Euclidea 2.2 Intersection of Angle Bisectors
2L is obvious. Here is the solution of 6E.
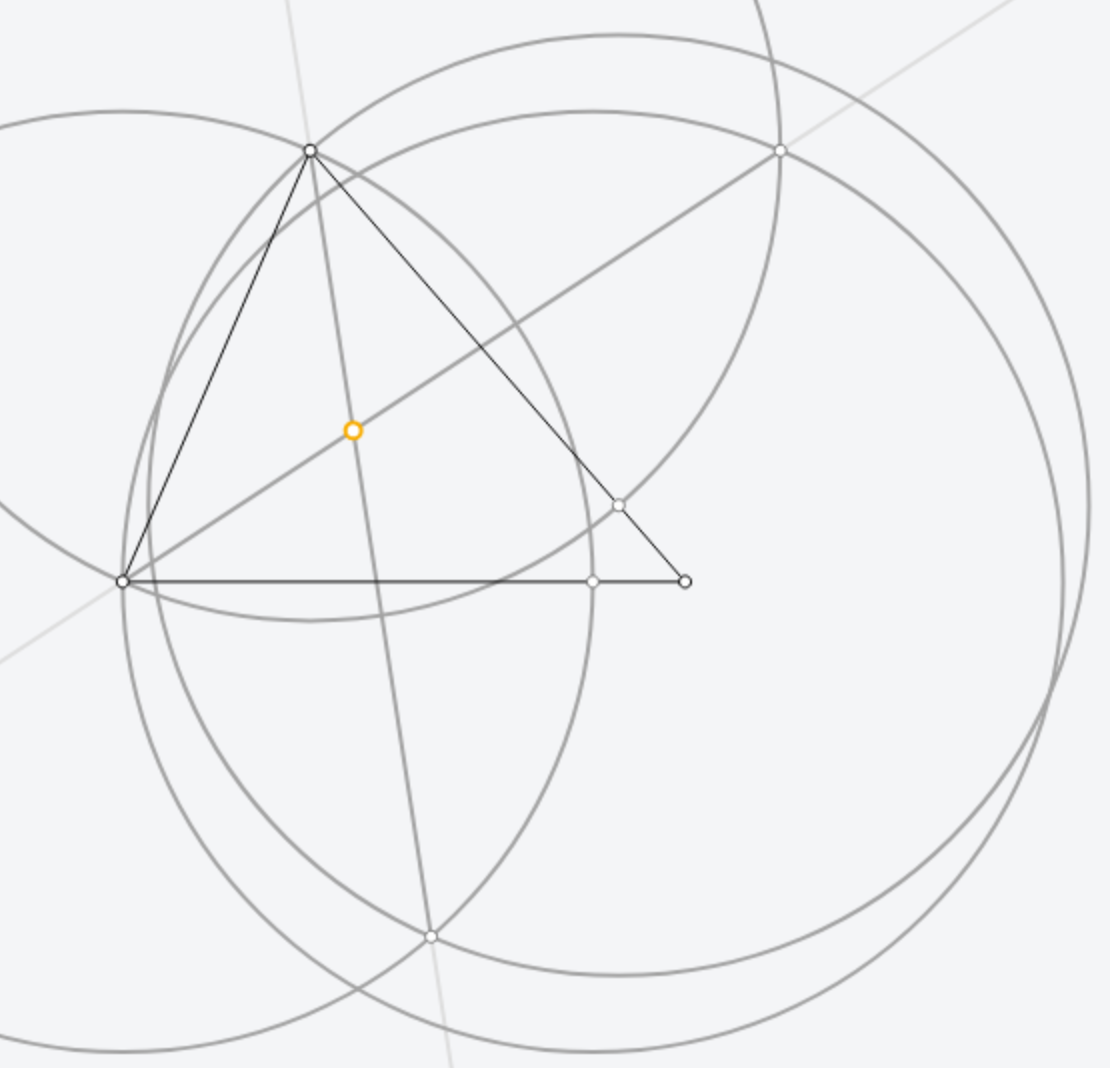
Detailed Steps
- Given triangle \(ABC\)
- Construct circle with center \(A\) and through \(B\). Circle intersect with \(AC\) at \(E\).
- Construct circle with center \(B\) and through \(A\). Circle intersect with \(BC\) at \(D\).
- Construct circle with center \(D\) and through \(B\). Circle intersect with circle \(A\) at \(F\).
- Construct circle with center \(E\) and through \(A\). Circle intersect with circle \(B\) at \(G\).
- COnstruct line \(AG\), \(BF\), intersect at \(I\).Point \(I\) is incenter of triangle \(ABC\).
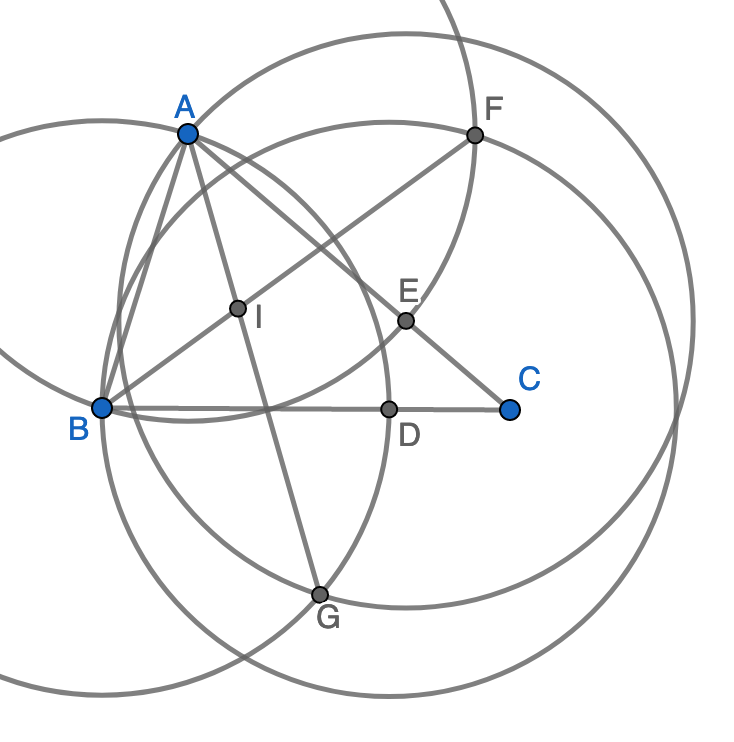
Proof for this problem is simple. If we only look at point \(BDFA\), then \(BF\) is obviously the angle bisector, similar for \(AG\). The trick here is to reuse as