Euclidea 1.7 Walkthrough

Euclidea 1.7 SquareInCircle

6L is obvious, here we focus on 7E. Solution is below.

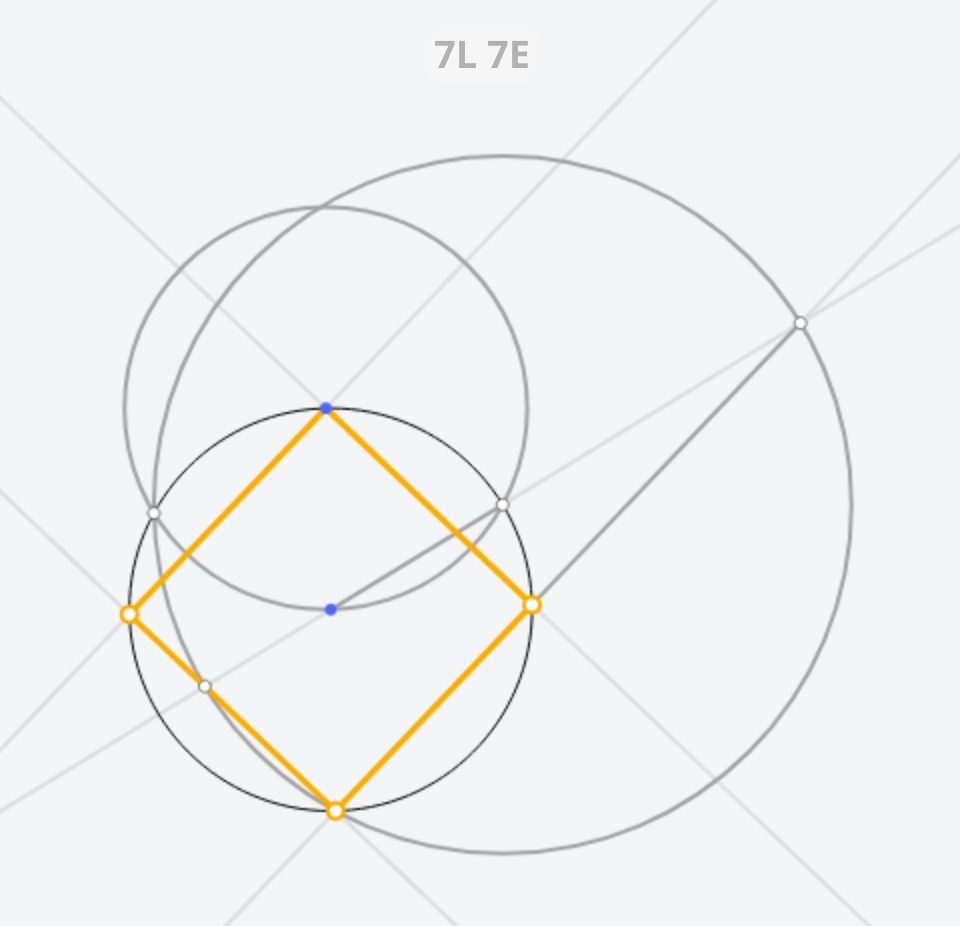
Detailed steps:

• Given circle \(A\) and vertex \(B\) .
• Construct a circle with center \(B\) through \(A\) . Two circled intersect at \(C, D\) .
• Construct a circle with center \(C\) and through \(D\) . Intersect with existing circles at \(F, J \)
• Construct line \(AC\) , intersect with circle \(A\) at \(H, E\)
• Construct segment \(EF\) and \(HF\) , intersecting with circle \(A\) at \(G, I\) .
• \(BGFI\) is the target square.

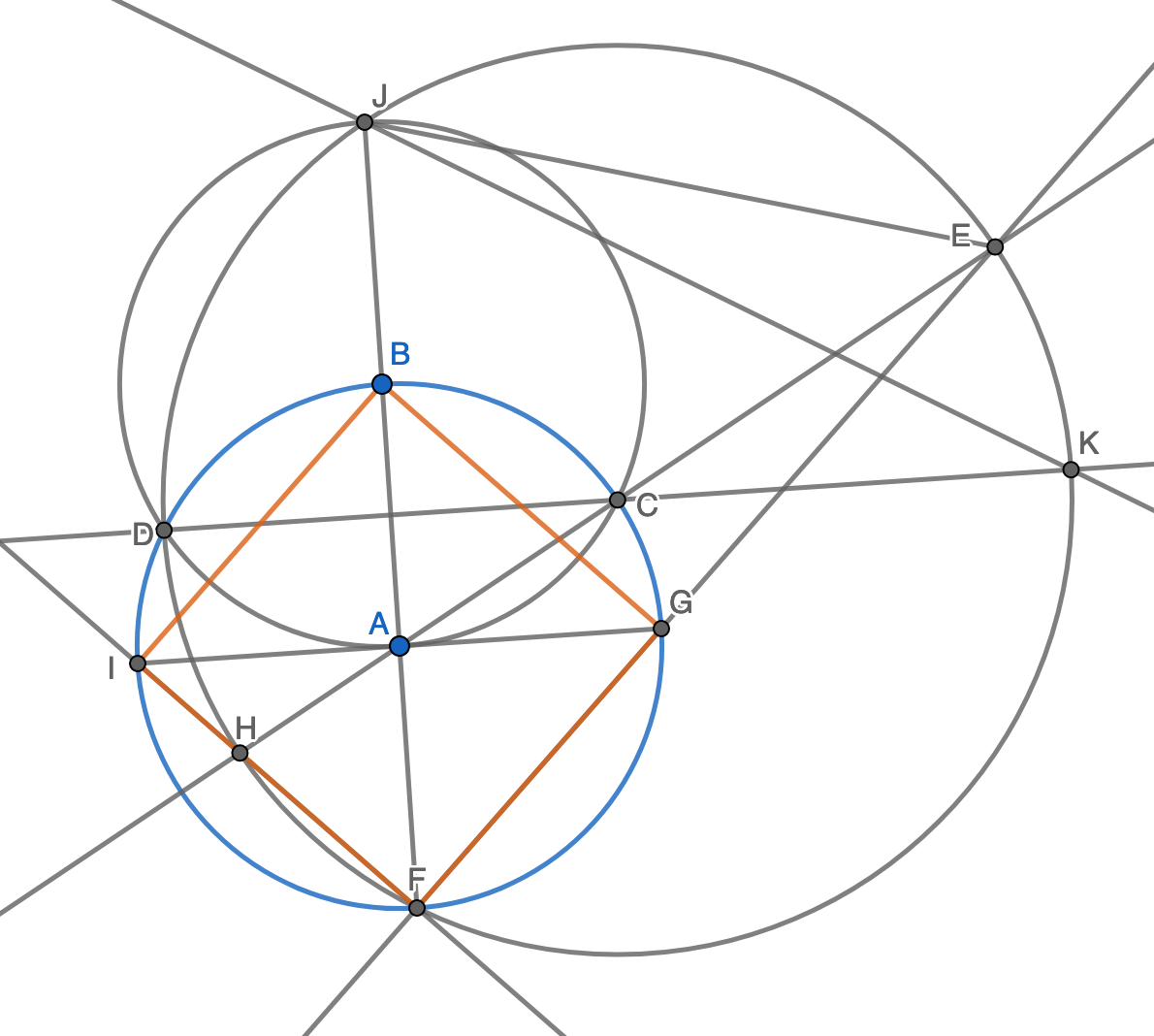
Proof:

• Construct line \(CD\) , intersecting circle \(C\) at \(K\) .
• In circle \(B\) , \(\angle DCA = \frac{1}{2} \angle DBA = 30^{\circ} \).
• \(\angle EJK=\frac{1}{2} \angle ECK = \frac{1}{2} \angle DCA = 15^{\circ}\). And \(\angle JEF = \angle JKF = 60^{\circ} \)，therefore \( \angle JFE = 45^{\circ}\).
• Obviously \(\triangle CBA\) and \(\triangle DBA\) are equilateral triangle, so we have \( \angle DAC = 120^{\circ}\). Assume BA intersect circle \(A\) at \(F'\), we have \( \angle CF'D = 60^{\circ} \). We also have \(F'C = F'D\) because \(C, D\) is symmetric against axis \(AB\). So we have \(DCF'\) as a equilateral triangle, then we have \(F'C = CD = CF\). So \(F' = F\) which means \(B, C, F\) are colinear.
• Since \(BF\) is diameter of circle \(A\)，\(\angle BGF = 90^{\circ}\). Thus, \(\triangle BGF\) is isosceles right triangle.
• And \( EH\) is diameter, therefore \(\angle EFH = 90^{\circ}\)。Similarly \(\triangle BIF\) is isosceles right triangle.
• Thus, rectangle \(BGFI\) is a square. Done.