Euclidea 2.4 Double Angle

We can achieve 3L and 3E in one go, as below:
Don't forget the 2V - one above and one under it.

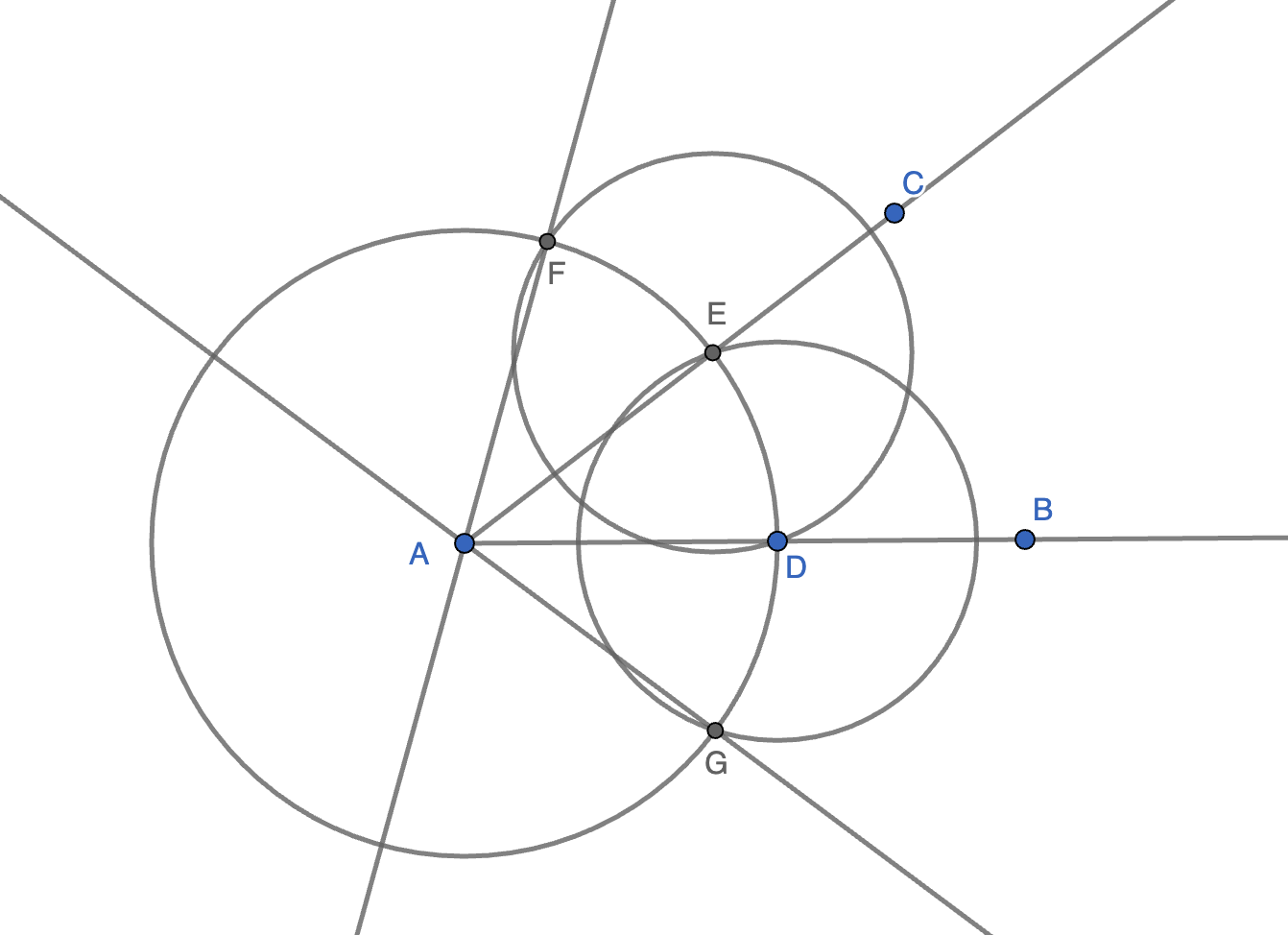
Detailed Steps

• We are given ray \(AB\) and \(AC\)
• From point \(A\), draw circle of any radius, intersecting \(AB\), \(AC\) at point \(D\), \(E\)
• Draw circle \(D\) pass point \(E\), intersect circle \(A\) at point \(G\). Point \(F\) is constructed similarly from circle \(E\)
• Connect \(AG\) and \(AF\), they are the doube angle we want.

Proof

• \(\triangle ADE\) and \(\triangle ADG\) are congurent.This can be proved by \(AE = AG\), and \(DE = DG\), since both pair of segments are constructed from circle.
• Thus, \(\angle DAE\) = \(\angle DAG\)