欧几里得-2.4: 二倍角

3L和3E可以一步到位.
别忘了2V - 上下各一个

详细步骤

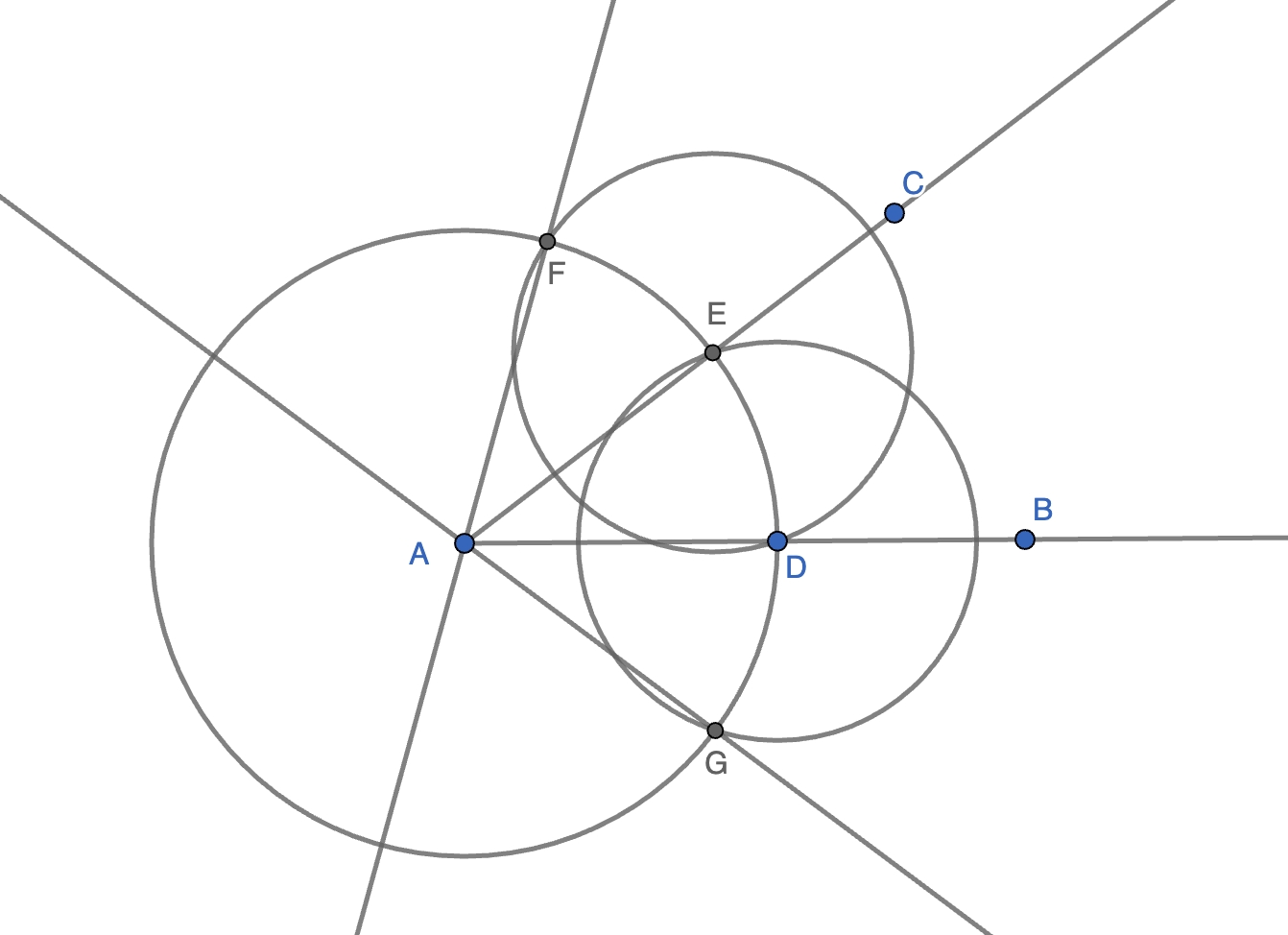
• 给定射线 \(AB\) 和 \(AC\)
• 以点 \(A\) 为圆心做任意圆, 交两射线于点 \(D\), \(E\)
• 以 \(D\) 为圆心,过 \(E\) 点做圆, 交圆 \(A\) 于 \(G\). 类似的做圆 \(E\) 得到点\(F\)
• \(AG\),\(AF\) 即为所求.

证明

• 三角形\(\triangle ADE\)和\(\triangle ADG\) 全等.这是由于从圆\(A\)出发有\(AE = AG\), 同理\(DE = DG\), 故而三边相等,即为全等三角形.
• 由全等易知\(\angle DAE\) = \(\angle DAG\)