欧几里得 1.7 内接正方形
6L显然,本文略。7E做法如下:
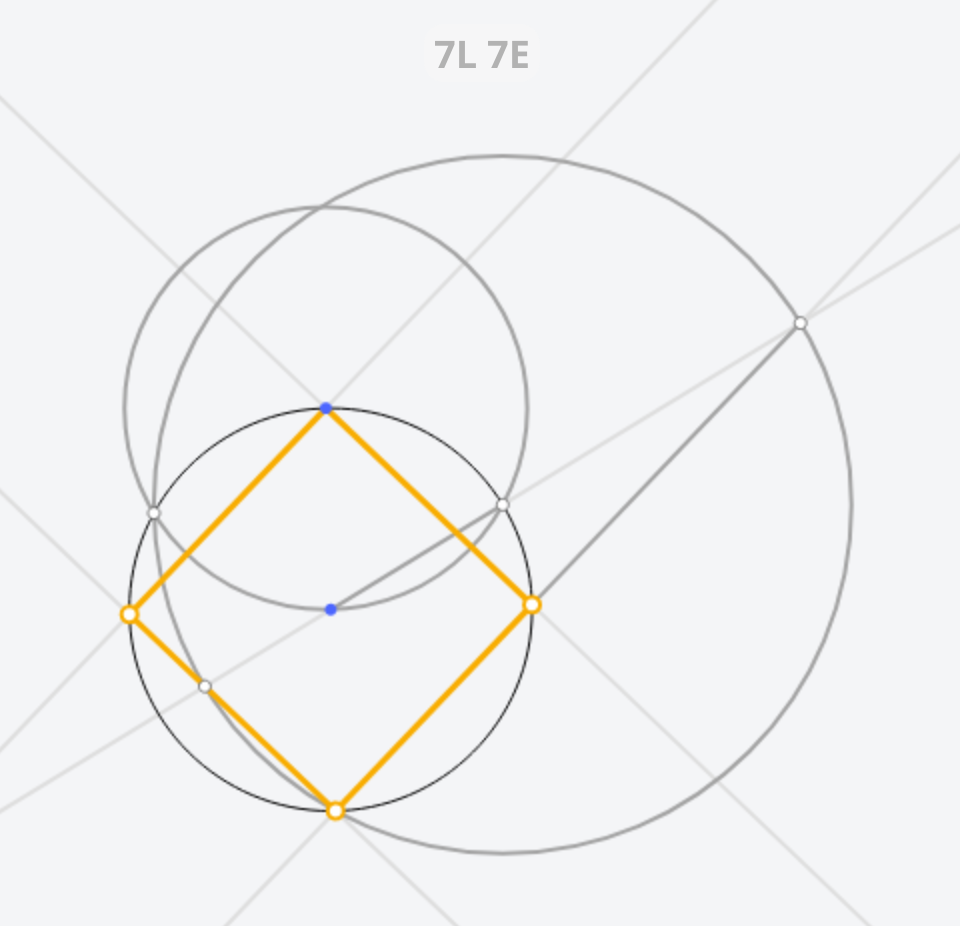
详细步骤:
- 给定圆\(A\)。
- 取\(A\)上的任意点\(B\),做过\(A\)的圆\(B\)。两圆交于\(C, D\)。
- 以\(C\)为圆心过点\(D\)做圆\(C\),交圆\(A\)于\(F\)。
- 延长\(AC\)交圆\(C\)于\(E, H\)。
- 连接\(EF\)交圆\(A\)于\(G\),连接\(HF\)交圆\(A\)于\(I\)。
- 四边形\(BGFI\)即为所求。
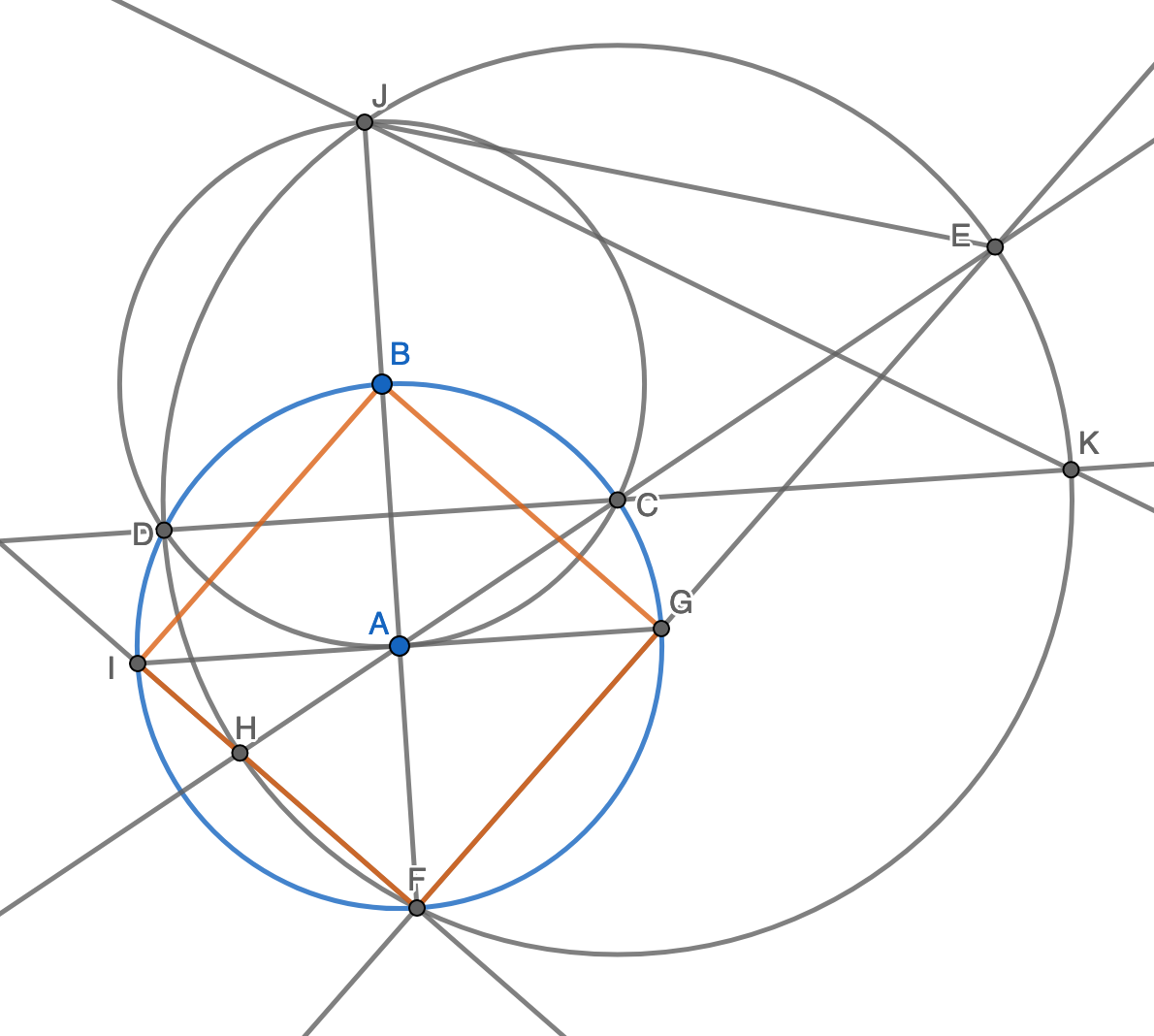
证明:
- 做圆\(C\)的直径\(DK\),\(\angle DCA = \frac{1}{2} \angle DBA = 30^{\circ} \) 。
- \(\angle EJK=\frac{1}{2} \angle ECK = \frac{1}{2} \angle DCA = 15^{\circ}\)。又因为\(\angle JEF = \angle JKF = 60^{\circ} \),所以\( \angle JFE = 45^{\circ}\)。
- 因为\(BF\)为圆\(A\)的直径, 所以\(\angle BGF = 90^{\circ}\)。所以\(\triangle BGF\)是等腰直角三角形。
- 又因为\( EH\)是直径,所以\(\angle EFH = 90^{\circ}\)。同理\(\triangle BIF\)是等腰直角三角形。
- 所以四边形\(BGFI\)是正方形。证毕。
若问,是不是没有证ABJF共线啊
确实跳过了这一步。
要证的话,角CFD是圆心角CAD的一半。另一方面BF作为直径可证两个直角三角形BFC和BFD,从而F是直径AB上的点。(不太严谨,大概思路这样)